ALJABAR BOOLEAN
Postulat sistem aljabar Boolean diperoleh
dengan cara membuat asumsi-asumsi dari tabel kebenaran gerbang logika.
6.1. Postulat Aljabar Boolean yang diturunkan dari
Gerbang logika
And
0 . 0 = 0
0 . 1 = 0
1 . 0 = 0
1 . 1 = 1
Or
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1
Not
6.2. Persamaan Aljabar Boolean turunan dari postulat dengan
1 variabel.
Postulat 1
diturunkan dari gerbang And
Pembuktian postulat 1.
Bila X = 0 maka, X . 0 = 0 . 0 = 0
Bila X = 1 maka, X . 0 = 1 . 0 = 0
Postulat 2
diturunkan dari gerbang And
Pembuktian postulat 2.
Bila X = 0 maka, X
. 1 = 0 . 1 = 0
Bila X = 1 maka, X
. 1 = 1 . 1 = 1
Postulat 3
diturunkan dari gerbang And
Pembuktian postulat 3.
Bila X = 0 maka, X
. X = 0 . 0 = 0
Bila X = 1 maka, X
. X = 1 . 1 = 1
Postulat 4
diturunkan dari gerbang And dan Not
Pembuktian postulat 4.
Bila X = 0 maka, X
.
= 0 . 1 = 0
Bila X = 1 maka, X
.
= 1 . 0 = 0
Postulat 5
diturunkan dari gerbang Or
Pembuktian postulat 5.
Bila X = 0 maka, X
+ 0 = 0 + 0 = 0
Bila X = 1 maka, X
+ 0 = 1 + 0 = 1
Postulat 6
diturunkan dari gerbang Or
Pembuktian postulat 6.
Bila X = 0, maka X + 1 = 0 + 1
= 1
Bila X = 1, maka X + 1 = 1 + 1
= 1
Postulat 7
diturunkan dari gerbang Or
Pembuktian postulat 6.
Bila X = 0, maka X + X = 0 + 0
= 0
Bila X = 1, maka X + X = 1 +
1 = 1
Postulat 8
diturunkan dari gerbang Or dan Not
Pembuktian postulat 8.
Bila X = 0 maka,
X +
= 0 + 1 = 1
Bila X = 1 maka,
X +
= 1 + 0 = 1
Variabel X pada postulat 1 sampai 8 dapat
dipakai untuk menyatakan suatu exspresi yang mengandung lebih dari satu
variabel.
Contoh
A
.
B = 0
Penyelesaian
Jika A
dianggap X
maka,
B =
Pada
postulat 4, X .
= 0 jadi A
.
B = 0
Dengan
cara yang sama semua postulat 1 sampai 8
dapat digunakan untuk menyelesaikan suatu ekspresi yang mengandung lebih dari
satu variabel seperti
6.3. Persamaan Aljabar Boolean turunan dari postulat dengan
Multivariabel.
Postulat 9 diturunkan dari hukum komutatif.
(9) X + Y = Y + X
Urutan variabel dalam suatu
penjumlahan tidak akan mengubah hasil penjumlahan.
Postulat 10 diturunkan dari hukum komutatif.
(10) X . Y = Y . X
Urutan
variabel dalam suatu perkalian tidak akan mengubah hasil perkaliannya.
Postulat 11 diturunkan dari hukum asosiaatif.
(11) X + (Y + Z)=
(X + Y) + Z = X + Y + Z
Pengelompokan
variabel dalam suatu penjumlahan dapat diubah sesuai dengan yang diinginkan tanpa merubah hasil
penjumlahannya.
Postulat 12 diturunkan dari hukum asosiaatif.
(12) X (YZ)= (X Y)Z = XYZ
Pengelompokan variabel dalam suatu perkalian dapat diubah
sesuai dengan yang diinginkan tanpa
merubah hasil perkaliannya.
Postulat 13 diturunkan dari hukum distributif.
(13) X + (Y + Z)=
(X + Y) + Z = X + Y + Z
Suatu
ekspresi dapat dijabarkan dengan cara mengalikan term demi term atau
menguraikan term demi term apabila ada dua atau lebih term yang mengandung
suatu variabel yang sama.
Contoh
A
C +
=
( A C +
)
A B C + A B D = A B ( C + D )
Contoh
soal dan penyelesaian
Sederhanakan persamaan,
1.
Y = A
D + A
Dengan menggunakan
Postulat 13 variabel-variabel A
dapat dikeluarkan
sehingga,
Y = A
(D +
)
Dengan
menggunakan Postulat 8 term dalam kurung nilainya = 1 jadi,
Y = A
(D +
) = A
. 1 = A
2.
Z = (
+ B ) ( A +
)
=
A +
+ B A + B
Dengan menggunakan Postulat 4 term-term
A dan B
nilainya = 0 jadi,
Z = 0 +
+ B A + 0
=
+ B A
6.4. Persamaan Aljabar Boolean turunan dari postulat
dengan pembuktian kasus.
Postulat 14 diturunkan dari pembuktian kasus
(14) X + (XY)= X
Pembuktian postulat 14.
Bila X = 0, Y = 0 maka, X +(X
Y) = 0 + (0 . 0 ) = 0
Bila X = 0, Y = 1 maka, X +(X Y) = 0 + (0 . 1 ) = 0
Bila X = 1, Y = 0 maka, X +(X Y) = 1 + (1 . 0 ) = 1
Bila X = 1, Y = 1 maka, X +(X Y) = 1 + (1 . 1 ) = 1
Pembuktian postulat 14 dapat juga dilakukan dengan postulat 6 sebagai
berikut,
X +(X Y) = X (1 + Y)
= X . 1 (disederhanakan dengan
postulat 6)
= X
(disederhanakan dengan postulat 2)
Postulat 15 (a) dan (b) diturunkan
dari pembuktian kasus
(15 a)
+ (
Y)=
+
Y
Pembuktian postulat 15(b).
Bila X =
0, maka X +(
Y) = X + Y = 0 + (1.
Y ) = Y
Bila X = 1, maka X
+(
Y) = X + Y = 1 + (0.
Y ) = 1
(15 b)
+ (XY)=
+ Y
Pembuktian postulat 15(a).
Bila X =
0, maka
+ (XY)=
+ Y = 1 + (0 . Y )
= 1 + 0 = 1
Bila X =
1, maka
+ (XY)=
+ Y = 0 + (1 . Y )
= 0 + Y = Y
Contoh Penyederhanaan
X = A C
D +
C D
= C D ( A +
B)
Variabel C D dikeluarkan
= C D ( A + B) dengan
postulat 15 a ( A +
B) diganti ( A + B)
=
A C D + B C D
6.5. Postulat Aljabar Boolean dari Teorema DeMorgan.
Postulat 16 diturunkan dari Teorema DeMorgan.
(16) ( X+Y )
= X
Komplemen dari suatu
penjumlahan Or sama dengan perkalian And dari komplemen-komplemennya.
Postulat 17 diturunkan dari Teorema DeMorgan.
(17) ( X.Y )
= X
Komplemen dari suatu perkalian
And sama dengan penjumlahan Or dari komplemen-komplemennya.
Penyederhanaan Fungsi Boolean Dengan Karnaugh Map
Setelah cukup memahami teorema aljabar Boolean, penyederhanaan fungsi Boolean dengan aljabar, dan model-model Karnaugh Map beserta pemetaannya, kini saatnya mencoba menyelesaikan fungsi logika Boolean dengan Peta Karnaugh (Karnaugh Map/ K-Map). Jika suatu fungsi logika memiliki tiga atau empat variabel, maka penyelesaian dengan K-Map ini akan lebih mudah dibanding dengan penyederhanaan cara Aljabar.
Dari beberapa model K-Map yang telah dibahas sebelumnya, penyederhanaan fungsi logika pada posting ini hanya akan menggunakan model-1 karena metode penyederhanaan dengan model-model K-Map lain pun hasilnya akan tetap sama.
Dari beberapa model K-Map yang telah dibahas sebelumnya, penyederhanaan fungsi logika pada posting ini hanya akan menggunakan model-1 karena metode penyederhanaan dengan model-model K-Map lain pun hasilnya akan tetap sama.
PENYEDERHANAAN DUA VARIABEL
Contoh 1.
F = AB + A'B + AB'
Penyelesaian:
F = AB + A'B + AB'
= A (B+B') + A'B
= A (1) + A'B
= A + A'B
= A + B (Teorema T9)
Perbandingan dengan software Karnaugh Map Explorer 1.0
Contoh 2.
F = AB' + A'B'
Penyelesaian:
F = AB' + A'B'
= (A+A') B'
= (1) B'
= B'
Perbandingan dengan software Karnaugh Map Explorer 1.0
PENYEDERHANAAN TIGA VARIABEL
Contoh 1.
F = ABC' + AB'C' + AB'C + ABC
Penyelesaian:
F = ABC' + AB'C' + AB'C + ABC
= AB (C'+C) + AB' (C'+C)
= AB (1) + AB' (1)
= AB + AB'
= A (B+B')
= A (1)
= A
Perbandingan dengan software Karnaugh Map Explorer 1.0
Contoh 2.
F = A'B'C + A'BC + AB'C + ABC + ABC'
Penyelsesaian
F = A'B'C + A'BC + AB'C + ABC + ABC'
= (A'+A)B'C + (A'+A)BC + ABC'
= (1) B'C + (1) BC + ABC'
= B'C + BC + ABC'
= (B'+B)C + ABC'
= (1) C + ABC'
= C + ABC'
= C + AB (Teorema T9)
= AB + C
Perbandingan dengan software Karnaugh Map Explorer 1.0
PENYEDERHANAAN EMPAT VARIABEL
F = A'BC'D + ABC'D + A'BCD + ABCD
Penyelsesaian
F = A'BC'D + ABC'D + A'BCD + ABCD
= (A'+A) BC'D + (A'+A) BCD
= (1) BC'D + (1) BCD
= BC'D + BCD
= BD (C'+C)
= BD (1)
= BD
Perbandingan dengan software Karnaugh Map Explorer 1.0
Contoh 1.
F = AB + A'B + AB'
Penyelesaian:
- Gambarkan K-Map Model-1 untuk dua variabel
- Ganti kotak-kotak yang sesuai untuk AB, A'B, dan AB, dengan angka satu (1) dan sisanya dengan angka nol (0)
- Gabungkan semua angka satu (1) sesederhana mungkin. Untuk mempermudah dapat menggunakan pemetaan K-Map dua variabel.
- Hasil penyederhanaan dari F = AB + A'B + AB' adalah F = A + B
F = AB + A'B + AB'
= A (B+B') + A'B
= A (1) + A'B
= A + A'B
= A + B (Teorema T9)
Perbandingan dengan software Karnaugh Map Explorer 1.0
Contoh 2.
F = AB' + A'B'
Penyelesaian:
- Gambarkan K-Map Model-1 untuk dua variabel
- Ganti kotak-kotak yang sesuai untuk AB' dan A'B' dengan angka satu (1) dan sisanya dengan angka nol (0)
- Gabungkan semua angka satu (1) sesederhana mungkin. Untuk mempermudah dapat menggunakan pemetaan K-Map dua variabel.
- Hasil penyederhanaan adalah F = B'
F = AB' + A'B'
= (A+A') B'
= (1) B'
= B'
Perbandingan dengan software Karnaugh Map Explorer 1.0
PENYEDERHANAAN TIGA VARIABEL
Contoh 1.
F = ABC' + AB'C' + AB'C + ABC
Penyelesaian:
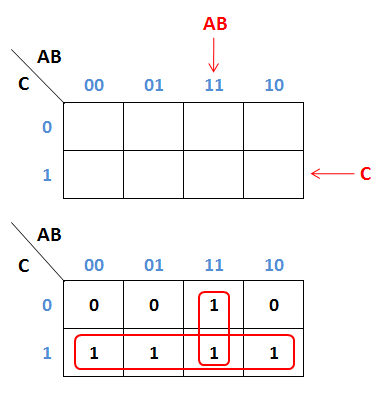
- Gambarkan K-Map Model-1 untuk 3 variabel kemudian tandai dengan angka satu (1) setiap kotak yang mewakili ABC', AB'C', AB'C, dan ABC, sisanya diisi dengan angka nol (0).
- Gambarkan pemetaan K-Map untuk 3 variabel yang paling mendekati dan paling sederhana. Pada kasus ini area A pada K-Map dapat mewakili semua variabel dalam soal.
- Hasil penyederhanaan dari F = ABC' + AB'C' + AB'C + ABC adalah F = A
F = ABC' + AB'C' + AB'C + ABC
= AB (C'+C) + AB' (C'+C)
= AB (1) + AB' (1)
= AB + AB'
= A (B+B')
= A (1)
= A
Perbandingan dengan software Karnaugh Map Explorer 1.0
Contoh 2.
F = A'B'C + A'BC + AB'C + ABC + ABC'
Penyelsesaian
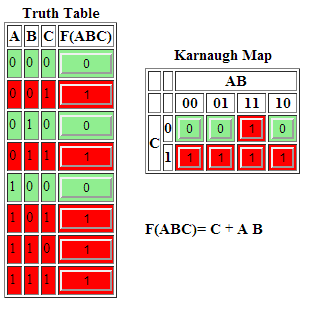
- Gambarkan K-Map Model-1 untuk 3 variabel kemudian tandai dengan angka satu (1) setiap kotak yang mewakili A'B'C, A'BC, AB'C, dan ABC, dan ABC', sisanya diisi dengan angka nol (0).
- Gambarkan pemetaan K-Map untuk 3 variabel yang paling mendekati dan paling sederhana. Pada kasus ini area AB dan area C pada K-Map dapat mewakili semua variabel dalam soal.
- Penyederhanaan dari F = A'B'C + A'BC + AB'C + ABC + ABC' adalah F = AB + C
F = A'B'C + A'BC + AB'C + ABC + ABC'
= (A'+A)B'C + (A'+A)BC + ABC'
= (1) B'C + (1) BC + ABC'
= B'C + BC + ABC'
= (B'+B)C + ABC'
= (1) C + ABC'
= C + ABC'
= C + AB (Teorema T9)
= AB + C
Perbandingan dengan software Karnaugh Map Explorer 1.0
PENYEDERHANAAN EMPAT VARIABEL
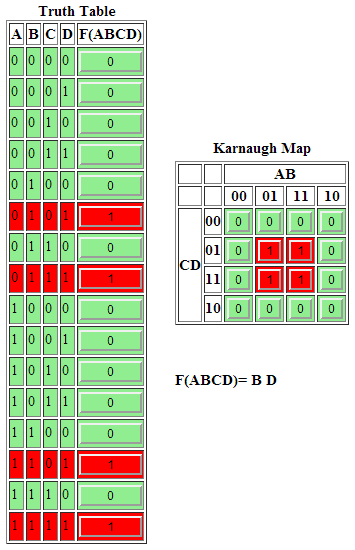
F = A'BC'D + ABC'D + A'BCD + ABCD
Penyelsesaian
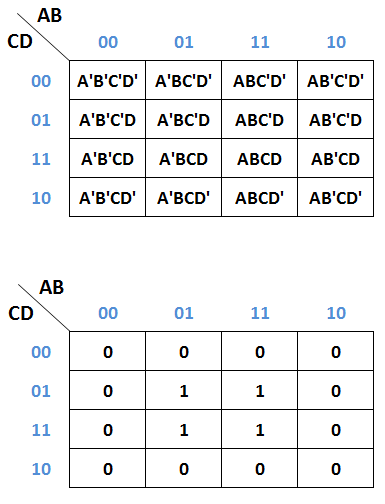
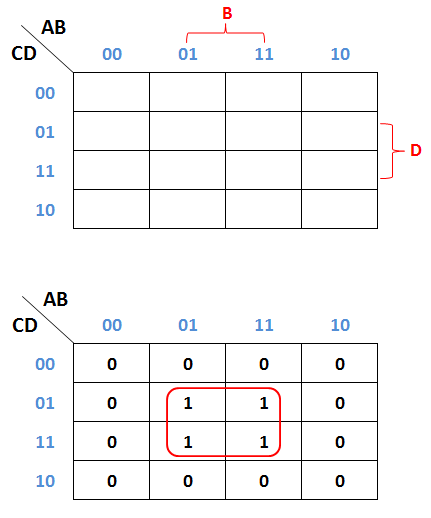
- Gambarkan K-Map Model-1 untuk 4 variabel kemudian tandai dengan angka satu (1) setiap kotak yang mewakili A'BC'D, ABC'D, A'BCD, ABCD, sisanya diisi dengan angka nol (0).
- Gambarkan pemetaan K-Map untuk 4 variabel yang paling mendekati dan paling sederhana. Pada kasus ini area B dab D pada K-Map dapat mewakili semua variabel dalam soal.
- Hasil penyederhanaan dari F = A'BC'D + ABC'D + A'BCD + ABCD adalah F = BD
F = A'BC'D + ABC'D + A'BCD + ABCD
= (A'+A) BC'D + (A'+A) BCD
= (1) BC'D + (1) BCD
= BC'D + BCD
= BD (C'+C)
= BD (1)
= BD
Perbandingan dengan software Karnaugh Map Explorer 1.0